あなたは、巨大地震が来ると思っていますか?
来ると思う人は、備えができていますか?
来ないと思う人は、その根拠がありますか?
地球の内部って、思ったより複雑なんだけど、
思ったよりも規則性があると私は考えているんですよ。

著者プロフィール
後藤忠徳(ごとう ただのり)
大阪生まれ、京都育ち。奈良学園を卒業後、神戸大学理学部地球惑星科学科入学。学生時代に個性的な先生・先輩たちの毒気に当てられて(?)研究に目覚める。同大学院修士課程修了後、京都大学大学院博士後期課程単位取得退学。博士(理学)。横須賀の海洋科学技術センター(JAMSTEC)の研究員、京都大学大学院工学研究科准教授を経て、2019年から兵庫県立大学大学院生命理学研究科教授。光の届かない地下を電磁気を使って照らしだし、海底下の巨大地震発生域のイメージ化、石油・天然ガスなどの海底資源の新しい探査法の確立をめざして奮闘中。著書に『海の授業』(幻冬舎)、『地底の科学』(ベレ出版)がある。個人ブログ「海の研究者」は、地球やエネルギーにまつわる話題を扱い評判に。趣味は、バイクとお酒(!)と美術鑑賞。

知識ゼロから学ぶ
地底のふしぎ
第2話
「マグニチュード9.0」ってなに?
文と絵 後藤忠徳
前回、私は「地球の中が分からないと困ることもある」と書きました。その代表例は巨大地震や火山噴火でしょう。まずは巨大地震について考えてみたいと思います。
すぐに思い出すのは、2011年に東日本大震災を引き起こした「東北地方太平洋沖地震」です。マグニチュードは9.0でした。このよく耳にする単語「マグニチュード」とはなんでしょうか? ニュースなどで「地震の規模を示すマグニチュードは…」と聞くことがあるので、なんとなく「マグニチュードが大きいと、大きな地震なんだ」ということは分かりますが、あらためて考えると、マグニチュードってなんだっけ? って方も多いと思います。まずはその辺りから話を始めてみましょう。なお以下に続く文章の所々で、マグニチュードを「M」と略しています。洋服やポテトのサイズではありません。
◎Lサイズなんてもんじゃない
「マグニチュード9.0」は本当に大きな地震です。まずは下の図1を見て下さい。地震計を用いて地震の大きさをちゃんと測れるようになってから約100年が経ちますが、そのあいだに起きた超巨大地震を地図上に描きました。太平洋の沿岸域で多く発生している様子がわかります。
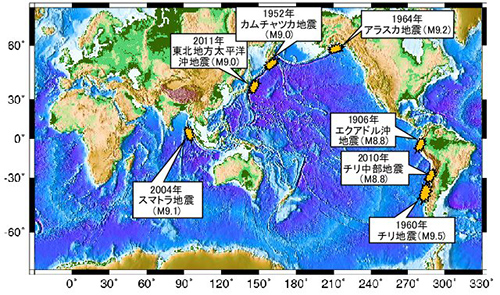
図1. 世界の超巨大地震の発生位置。表1の1位~6位(合計7つ)の地震を地図上に表示。「NHK そなえる防災」コラム(2012年7月:大地震は火山噴火を誘発する!?:http://www.nhk.or.jp/sonae/column/20120622.html)に基づきました。ただしマグニチュードは表1に準じています。
(http://www.jma.go.jp/jma/kishou/know/faq/faq7.html より)
次のアメリカ地質調査所のホームページに基づいています。
(http://earthquake.usgs.gov/earthquakes/world/10_largest_world.php)
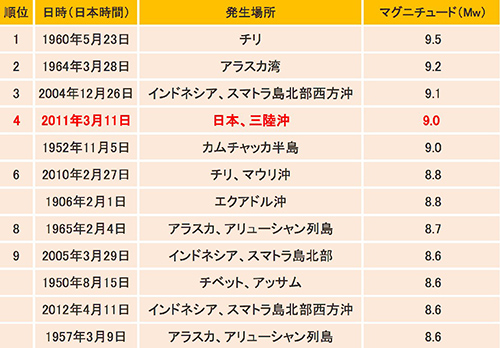
次に、最近約100年間に起きた地震の大きさランキングも見てみましょう(表1) 。1位はいまから約50年前の1960年に起きたチリ地震でM9.5です。2位はやはり約50年前のアラスカ地震(M9.2)。3位は記憶にも新しい、2004年のスマトラ地震(M9.1)。そして4位が東北地方太平洋沖地震(M9.0)。同じく4位のカムチャツカ地震とあわせても、過去100年間でM9.0以上の超巨大地震は5回しか起きていません。
ちなみにM8.0以上の地震は「巨大地震」、M9.0クラスの地震は「超巨大地震」と呼ばれることがありますが、この分類にきちっとした決まりはありません。
◎1つMが増えると32倍のエネルギー
なるほど、M9.0の地震が超巨大であることは分かりますが、まだピンときません。具体的にどれくらい大きいのか。マグニチュードとはそもそも地震が放出したエネルギーを表す指標ですが、マグニチュードが「1つ」増えると地震のエネルギーは「約32倍」増えます。マグニチュードが「2つ」増えると地震のエネルギーは「1000倍」になります……ややこしいですね。でも大小さまざまな地震があるということは、そのときに放出されるエネルギーにも何桁もの差があるということです。
「今回の地震の大きさは、前回の地震の約32,000,000倍でした」というニュース原稿を読むアナウンサーを想像してみてください。お世辞にも便利とは言いがたいので、「1増えると○倍増える」という方式が地震の大きさを示す指標として採用されています。
似たような単位の例としては、音の大きさなどを表すデシベルが挙げられます。10デシベル増えると音の大きさは約3.2倍に、20デシベル増えると10倍に増えます。
◎比べてみると……
試みにM9.0の東北地方太平洋沖地震のときに放出されたエネルギーを何かと比べてみましょうか。例えば、1995年に阪神・淡路大震災を引き起こした兵庫県南部地震(M7.3)とはどれくらいの差があるのでしょうか?
この地震も神戸の市街地などに大きな被害をもたらしました(本連載でも改めて取り上げます)。M7.3とM9.0ではマグニチュードの差は1.7です。ということは、東北地表太平洋沖地震で放出されたエネルギーは、兵庫県南部地震の約5倍? 10倍?……いえいえ、計算してみると、なんと約350倍に相当します(注1)。あの神戸の地震350個分がほぼ同時に起きたのが東北地方太平洋沖地震なのです。

私たちが普段使っている電気エネルギーとも比較してみましょう。計算式は末尾(注2)に書くとして、結論をもう言っちゃいましょう。日本全体で約6か月間に使う全電気エネルギーとM9.0の地震が放出するエネルギーが同じくらいです(図2)。
東北地方太平洋沖地震の発生から終わりまではわずか数分間ですから、その短い時間に6か月分の電気エネルギーを一気に使い果たしたようなものです。
あるいは(物騒ですが)爆弾と比べてみましょう。第二次世界大戦の際に広島市に落とされた原子爆弾が放った全エネルギーはマグニチュード6の地震が放つエネルギーと同じくらいと言われています。M9.0とM6.0では約32,000倍のエネルギーの差がありますから、M9.0の地震が放出するエネルギーは広島型原子爆弾3万個分のエネルギーを上回るのです。
◎地面のずれ方が全然違う
地震のエネルギーが異なるということは、地震の際の地面のずれ方も異なります。前回も少し書きましたが、地震とは、地下の岩石が壊れて、ずれ動く現象です。一方、大地がずれ動いてできた傷跡は「断層」と呼ばれています。すなわち「断層がずれ動いて地震が発生するのだ」と考えられています(図3)。
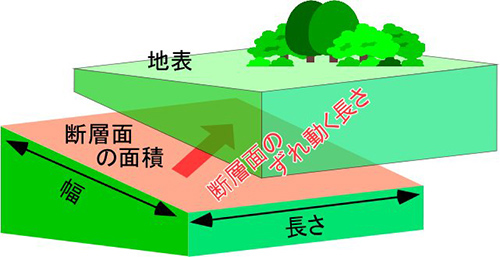
断層がずれて地震が起きるとき、放出されるエネルギーは「断層の長さ×断層の幅×断層のずれ動く長さ」に比例することが知られています。長くて広い断層面が大きくずれ動くほど、マグニチュードの大きな地震が発生するのです。
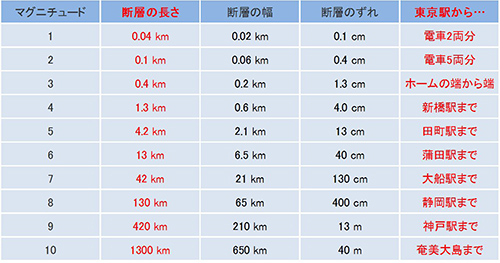
マグニチュードが1つ増えると、断層の長さ・幅・断層のずれはそれぞれ約3倍になります。目安として、表2にマグニチュードと断層のサイズの関係をまとめました。実際には、狭めで長い断層で地震が発生したり、断層の面積に比べてずれる量が大きかったりと、地震一つひとつにも個性がありますから、表2の数値はあくまで目安です。
とはいえ、例えばM4.0の地震を引き起こす断層のサイズと、M9.0を引き起こす断層のサイズには、これほどの違いがあることに驚く方もおられることでしょう。M4.0の地震は東京駅から新橋駅まで続くような短い断層がずれて発生しますが、M9.0の地震が起きるためには東京駅から神戸駅まで続くような大断層が一気にずれ動かねばなりません。
◎海底に、東京−神戸間より長い大断層
実際、東北地方太平洋沖地震の際には、何百kmにも及ぶ長さの断層がずれ動きました。2011年3月11日14:46、東北地方の太平洋側の沖合の海底の下でM9.0の地震が発生しました(これを本震と呼びます。一連の地震活動の中でもっとも大きかったものを指しています)。海底で巨大な断層がずれ動き、超巨大地震が発生したのです。
断層ではその後、余震が発生しました。余震とは本震の発生後に本震の周辺で発生する地震です。余震は本震からはるか離れた内陸部分や日本海側でも起きましたが、多くは太平洋側の海底の断層面上で発生しました。この余震の分布から、海底の断層の長さは約550km(南北方向)、幅は約200km(東西方向)に及ぶことが明らかになっています(図4)。
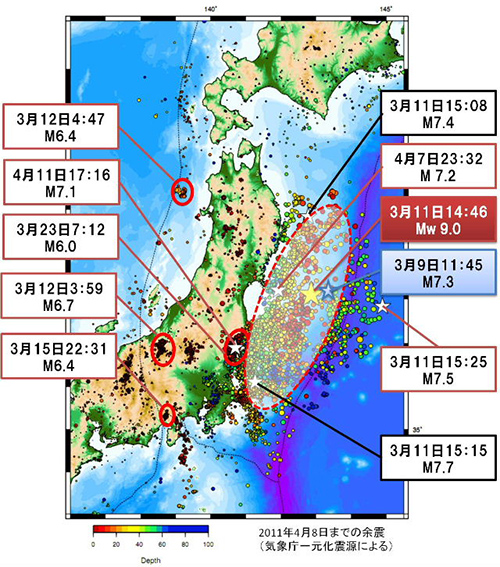
http://outreach.eri.u-tokyo.ac.jp/eqvolc/201103_tohoku/
◎Mのナゾ
ところで東北地方太平洋沖地震はM9.0という超巨大地震だったのですが、このマグニチュードは何回か修正されています。気象庁は最初この地震のマグニチュードを「7.9」と速報しましたが、すぐに「8.4」へ修正。ところがその後「8.8」へ修正し、さらに「9.0」へと再修正しています。一度発表したマグニチュードを修正するとは、なにかあったに違いありません。なぜマグニチュードは修正されたのでしょう?
マグニチュードのお話、次回に続きます。
注1:マグニチュードがmだけ異なる場合、地震のエネルギーは10の(1.5×m)乗違うことが知られています。m=1.7の場合、10の2.55乗となり、約355倍の違いになります。 iPhoneの計算機を横にすると関数電卓になるので実際に計算してみてください。
注2:電気事業連合会によると2012年(1年間)の日本全体の総電力消費量は9408億kWhでした。(電源別発電電力量構成比: http://www.fepc.or.jp/about_us/pr/sonota/__icsFiles/afieldfile/2013/05/17/kouseihi_2012.pdf) これに基づくと日本全体では24時間平均で、1秒あたり9408÷(24×365)= 約1.1 億kWの電力を消費しています。9分間では約580 億kW秒=約6.0×10の13乗 J(ジュール)。これはM6.0 の地震が放出するエネルギーとおおよそ同じ値です。同様に6ヶ月間では約1700兆kW秒=約2.0×10の18乗J。これはM9.0の地震が放出するエネルギーに匹敵します。

【バックナンバー】
第1話 世界一深い穴でもまだ浅いのだ

